《勾股定理》PPT下载
第一部分内容:学习目标
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想。(重点也是难点)
2.会用勾股定理进行简单的计算 。(重点)
... ... ...
勾股定理PPT,第二部分内容:勾股定理的历史
勾股定理有着悠久的历史:古巴比伦人和古代中国人看出了这个关系(即直角三角形三边关系),古希腊的毕达哥拉斯学派首先证明了这个关系。
勾股定理被誉为“人类最伟大的十个科学发现之一”,是初等几何中的一个基本定理。在我们今后的几何计算题和推理题中都有着广泛的应用。
勾股定理也有很多别称,也叫毕达哥拉斯定理、百牛定理、商高定理、驴桥定理和埃及三角形等。
迄今为止,勾股定理大约有500多种证明方法,是证明方法最多的定理之一。
... ... ...
勾股定理PPT,第三部分内容:探究新知
勾股定理的认识及验证
相传2500多年前,毕达哥拉斯在朋友家做客时,看到朋友家用砖铺成的地面图案,发现了直角三角形三边的某种关系(如图):
问题1 试问正方形A、B、C面积之间有什么样的数量关系?
问题2 图中正方形A、B、C所围成的等腰直角三角形三边之间有什么数量关系?
等腰直角三角形三边的关系为:两直角边的平方和等于斜边的平方。
问题3 网格中为一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?(每个小正方形的面积为单位1):
方法1:补形法(把正方形C补成各边都在网格线上的正方形):
方法2:分割法(把正方形C分割成易求出面积的三角形和四边形):
由上面的几个例子,我们不难得到这样的猜想:
命题1 如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2.(即直角三角形两直角边的平方和等于斜边的平方.)
... ... ...
勾股定理PPT,第四部分内容:归纳总结
现在,我们已经证明了命题1的正确性,在数学上,经过证明被确认为正确的命题叫做定理,所以我们刚刚猜想的命题1在我国叫做勾股定理.
勾股定理: 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.(即直角三角形两直角边的平方和等于斜边的平方).
... ... ...
勾股定理PPT,第五部分内容:新知应用
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
... ... ...
勾股定理PPT,第六部分内容:当堂练习
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
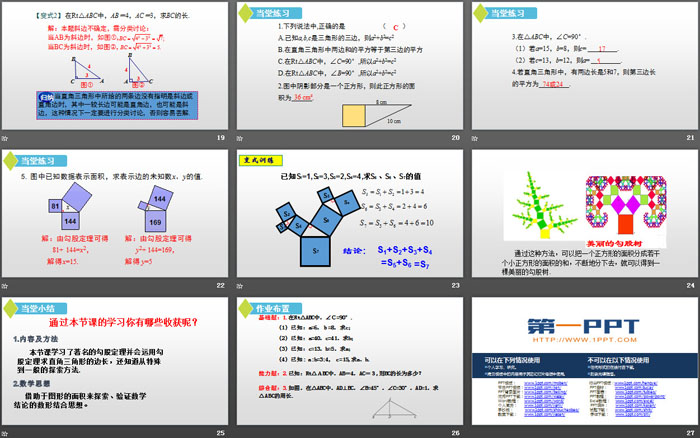
2.图中阴影部分是一个正方形,则此正方形的面积为_______.
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c=_________.
(2)若c=13,b=12,则a=_________ .
4.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
... ... ...
勾股定理PPT,第七部分内容:当堂小结
通过本节课的学习你有哪些收获呢?
1.内容及方法
本节课学习了著名的勾股定理并会运用勾股定理求直角三角形的边长,还知道从特殊到一般的探索方法.
2.数学思想
借助于图形的面积来探索、验证数学结论的数形结合思想。
... ... ...
勾股定理PPT,第八部分内容:作业布置
基础题:1.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
能力题:2.已知:Rt△ABC中,AB=4,AC=3,则BC的长为多少?
综合题:3.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
关键词:人教版八年级下册数学PPT课件免费下载,勾股定理PPT下载,.PPT格式;
更多关于《 勾股定理 》PPT课件, 请点击 勾股定理ppt标签。
《勾股定理》PPT(第3课时利用勾股定理作图和计算):
《勾股定理》PPT(第3课时利用勾股定理作图和计算) 第一部分内容:知识要点 1.勾股定理与数轴、坐标系 2.勾股定理与网格 3.勾股定理与几何图形 新知导入 想一想: 我们知道数轴上的点..
《勾股定理》PPT(第2课时勾股定理的应用):
《勾股定理》PPT(第2课时勾股定理的应用) 第一部分内容:知识要点 1.利用勾股定理解决实际问题 2.构造直角三角形解决实际问题 新知导入 看一看:观察下图中物体的运动过程,试着计算..
《勾股定理》PPT(第1课时):
《勾股定理》PPT(第1课时) 第一部分内容:知识要点 1.勾股定理 2.勾股定理与图形面积 新知导入 相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形..